Navigation:
Size-Extensivity
A method is said to be size-extensive if it gives the energy of a group of $N$ non-interacting replicas of a system as $E(N) = N E(1)$, where $E(1)$ is the energy of a single system. So, if we have a group of $N$ helium atoms placed infinitely far apart from each other (i.e., non-interacting), the total energy should be $N$ time the energy of a single helium atom.
This may sound like an obvious property, but it is not satisfied by some approximate electronic structure methods. This has consequences for finite systems even though it is not possible to make a formal definition for size-extensivity for finite systems. But one observation is that as the system gets larger (more electrons), a method that is not size-extensive will lead to increasingly larger errors in the correlation energy.
The Question
Which of the following methods are size-extensive?
- - RHF - UHF - MP2 - CISD
In this lab you will use the skills you have learned so far to set up calculations to answer this question.
Guidance
Consider the following issues when setting up your calculations:
- Which system? It needs to be small enough to allow easy calculation of the energy of multiple copies. So choose the rare gas atoms or a small molecule like water. The choice is yours.
- How to make, say, two copies of your system non-interacting? Place them far apart. How far? In principle you could compute the energy of the pair for ever increasing separations till the interaction energy became nearly zero. Whatever you choose for the inter-system separation, justify the choice.
- Basis set: it can't be too small or too large. I suggest something like cc-pVDZ.
How many replicas? Well, you need to do this for different values of $N$.
Essentially, if you make a plot of $E(N)/E(1)$ vs $N$ you should get a straight line with slope $1$. Alternatively, $E(N)/N$ should be a constant. So this gives you two possible ways of evaluating the data you will accumulate.
But also see how it is done by Helgaker et al. They cover size-extensivity in chapter 11, in sec. 11.2.4. Have a look at this chapter and see if you can adapt it to your needs. Here is one of the figures from this chapter. Here they plot the correlation energy per water molecule as a function of the number of (non-interacting) water molecules:
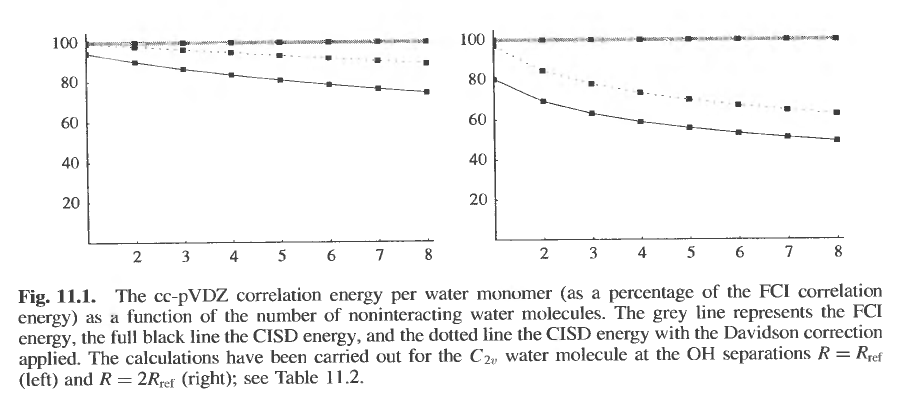
In case you have forgotten, the correlation energy is defined as $E_{\rm corr} = E - E_0$, where $E$ is the exact energy (unknown, but approximated by the correlated method used, and $E_0$ is the HF energy.
How will you be assessed?
Your work will be assessed by the justification you put into your numerical choices and how you analyse them. You are free to discuss, consult Helgaker or any other book, or ask me questions. But your analysis and short (2 pages) report should be done yourself.
You can complete the lab at home if needed.
Record the following in your writeup:
- Numerical choices
- Justification for these.
- System choice/s and justification.
- Raw data in tables.
- Graphs
- Analysis
You are not required to write more than 2 pages (data tables are excluded from this count).
