Index:

• Topics in Intermolecular Interactions

Symmetry-Adapted Perturbation Theory

Until recently, and possibly still so for certain applications, one of the most successful perturbation theories for intermolecular interactions was the symmetry-adapted perturbation theory (SAPT)¹. SAPT is a triple perturbation theory based on a Hartree-Fock description of the interacting monomers. Intramolecular correlation is built up using two of the perturbations, and intermolecular correlation by the third. SAPT has been applied to a large number of systems with very good success. However, SAPT, like the CCSD(T) method, is computationally expensive with scaling of $\mathcal{O}(N^7)$, where $N$ is the size of the system (which can be taken to be the number of electrons), and quickly become impossible to apply as this size increases, and cannot be applied to systems of more than about 10 atoms without a significant reduction to the level of correlation.

Symmetry-adapted perturbation theory based on DFT

Fairly recently, Szalewicz, Misquitta & Jeziorski²,and independently, Jansen & Hesselmann ³ developed a variant of SAPT based on DFT that has largely superseded SAPT both in terms of accuracy as well as computational efficiency. In this method, termed SAPT(DFT) or DFT-SAPT, the interaction energy components are formulated to make their dependence on molecular properties like the charge density and density response functions explicit. These molecular properties are then calculated using DFT and linear-response time-dependent DFT. In some sense, DFT is used to describe intramolecular correlation effects, thereby significantly simplifying the perturbation theory as the intramolecular perturbation operators are no longer required.

The first-order electrostatic energy $E_{\rm elst}^{(1)}$ has already been shown to arise from the Coulomb interaction of the unperturbed total charge densities of the interacting monomers. In SAPT(DFT), these densities are obtained from DFT. To see how the second-order induction and dispersion energies can be expressed in terms of molecular properties we need to define the frequency-dependent density susceptibility (FDDS): $ \alpha_{X}(r, r'|\omega) = 2 \sum_{r \ne 0} \frac{E^{X}_{r} - E^{X}_{0}}{ (E^{X}_{r} - E^{X}_{0})^2 - \omega^2 } \langle \Phi^{X}_{0}|\hat{\rho}_{X}(r) |\Phi^{X}_{r} \rangle \langle \Phi^{X}_{r}|\hat{\rho}_{X}(r')|\Phi^{X}_{0} \rangle, \label{eq:FDDS} $ where $\omega$ is a frequency and $\hat{\rho}_{X}(r) = -\sum_{i \in {X}} \delta(r - r_{i})$ is the electron density operator. The FDDS describes the linear response of the electron density to a frequency-dependent perturbation.

$E_{\rm ind,pol}^{(2)}(A)$ can be written in terms of the FDDS evaluated at zero frequency ⁴: $ E_{\rm ind,pol}^{(2)}(A) = -\frac{1}{2} \iint V_{B}(r) \alpha_{A}(r, r'|0) V_{B}(r') dr dr' \label{eq:EindFDDS} $

where $V_{B}(r) = \int \rho^{\rm tot}_{B}(r')/|r-r'|dr'$ is the electrostatic potential of monomer B, and similarly for $E_{\rm ind,pol}^{(2)}(B)$. We therefore see that the induction energy is a //response// energy of the molecule to the potential arising from the interacting partner.

The dispersion energy involves the FDDSs of the two molecules evaluated at imaginary frequency ⁵:

$ E_{\rm disp}^{(2)} = -\frac{1}{2\pi}\int_0^\infty d\omega \int dr_1 dr'_1 dr_2 dr'_2 \frac{\alpha_{A}(r_1,r'_1;i \omega) \alpha_{B}(r_2,r'_2;i \omega)}{|r_1-r_2||r'_1-r'_2|}.\label{eq:EdispFDDS} $

There is no easy way to interpret this expression which is a coupling of the response functions of the two molecules, but at imaginary frequency. However see the discussions by Angyan and Hessemlann ⁶ where an approximate form of this expression is related to correlations in fluctuating exchange-holes of the monomers. Also see the physical explanation I have provided in our discussion of the energy components.

There are exchange terms too and these are approximate - though very accurate - in SAPT(DFT). The expressions for these terms are much more complex that those given above so I will not provide them here.

What's important in the above discussion is that, //in principle//, SAPT(DFT) gets the non-exhange components exactly //as long as the density and density responses obtained from DFT are exact//. Of course, this is a tall order and these quantities are never going to be exact. 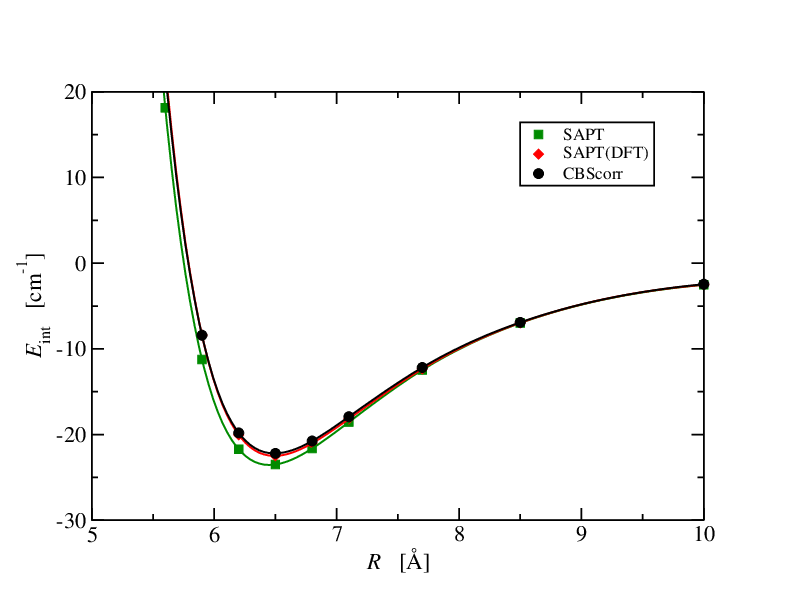Still SAPT(DFT) does very well and, as you have seen in the examples provided, is comparable to CCSD(T) - the //gold standard// of quantum chemistry. Here is another example to support this assertion. The He$\cdots$CO system: In this example the reference energies are obtained from basis-set extrapolated CCSDT (that's full triples). Data are from Kirk Peterson's group. The SAPT(DFT) energies are spot on. SAPT is somethat too deep.