Index:

• Topics in Intermolecular Interactions

DFT in SAPT(DFT)

Which exchange-correlation functional should be used in SAPT(DFT) calculations? The short answer is that while SAPT(DFT) interaction energies are not very sensitive to the exchange-correlation functional used, it has been concluded from extensive numerical experiments that the asymptotically corrected ¹ PBE0 ² exchange-correlation functional results in the most accurate interaction energies for a variety of systems.

The PBE0 functional (also called PBE1PBE) is a hybrid functional with 75% of its exchange energy determined from PBE and 25% from the so-called exact, or Hartree-Fock exchange. This means that the FDDS must also be constructed as the hybrid of the FDDSs from CKS and CHF theories. This is quite important as significant errors in the dispersion energy are introduced if the FDDS is constructed using CKS theory alone ³. For large molecules however, the terms in FDDS that depend on the functional derivative of the exchange-correlation potential are computationally demanding to evaluate using the PBE functional. Instead, a more practical approach is to calculate these coefficients using the exchange-only LDA functional. Therefore, while the Kohn-Sham molecular orbitals and eigenvalues are obtained using the PBE0 functional, the FDDS is best constructed using the less accurate LDA+CHF kernel. This approximation results in a small (less than 1%) loss in accuracy which is more than compensated by an order of magnitude reduction in computational expense.

The Asymptotic Correction

One of the problems with conventional density functionals is that they exhibit what is known as a //self-interaction error//. That is, when an electron is pulled off a molecule, instead of experiencing a $-1/r$ potential arising from the hole it has left behind, in standard DFT it will see a potential that vanishes exponentially quickly with distance. That is, it will see itself (or a fraction of itself): hence the name //self-interaction error//. 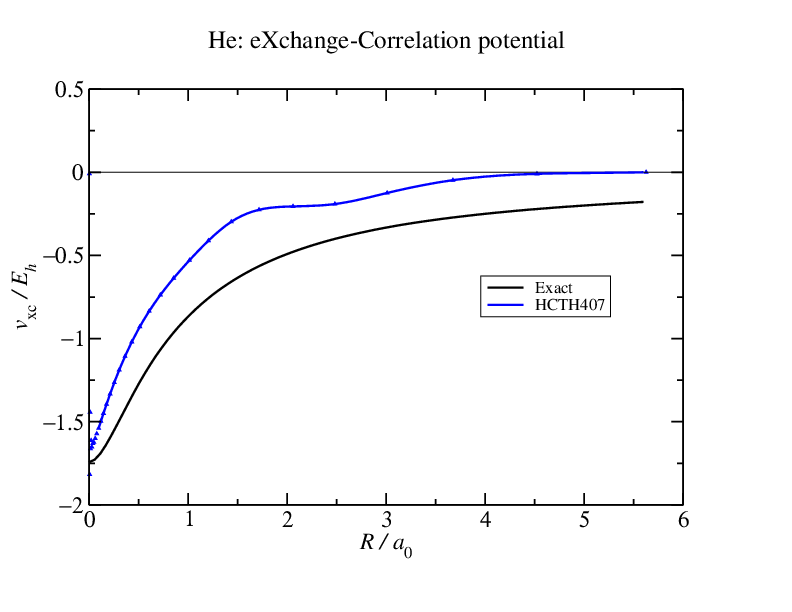Here's the Kohn-Sham exchange-correlation potential for helium calculated with the HCTH407 functional and also what is essentially the exact potential. Notice that

• The exact potential decays gently as $-1/r$ as it should.

• The HCTH407 potential is //shifted// away from the exact result and it decays too quickly.

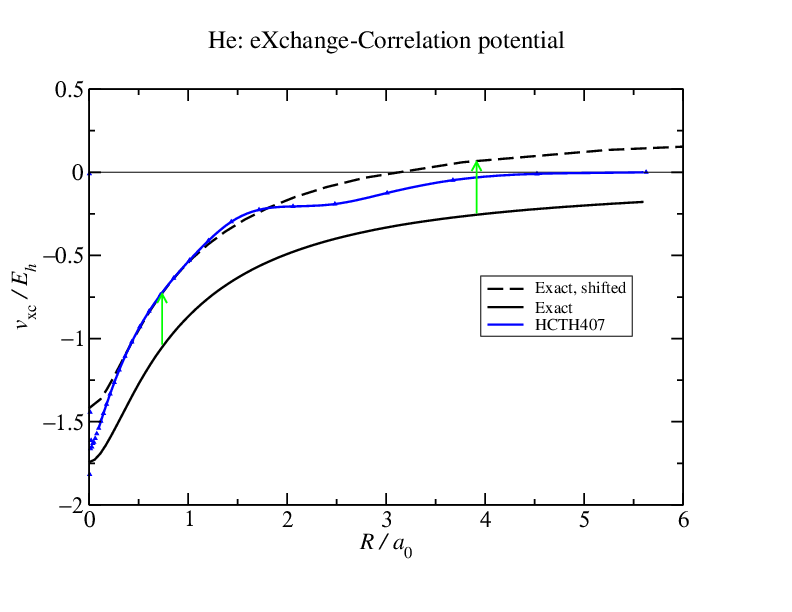This is more easily evident in the second figure where I have moved the exact potential up to better match the HCTH407 one.

Does this potential matter very much? Yes it does. The constant shift is not consequential, but the shape difference is. The HCTH407 potential decays too quickly so charge density slops out and the helium density becomes over diffuse. This means that any quantity dependent on the density tails (all of the interaction energy components, polarizabilities, multipole moments,...) will be effected and the effect could be large enough that the results are not very useful. 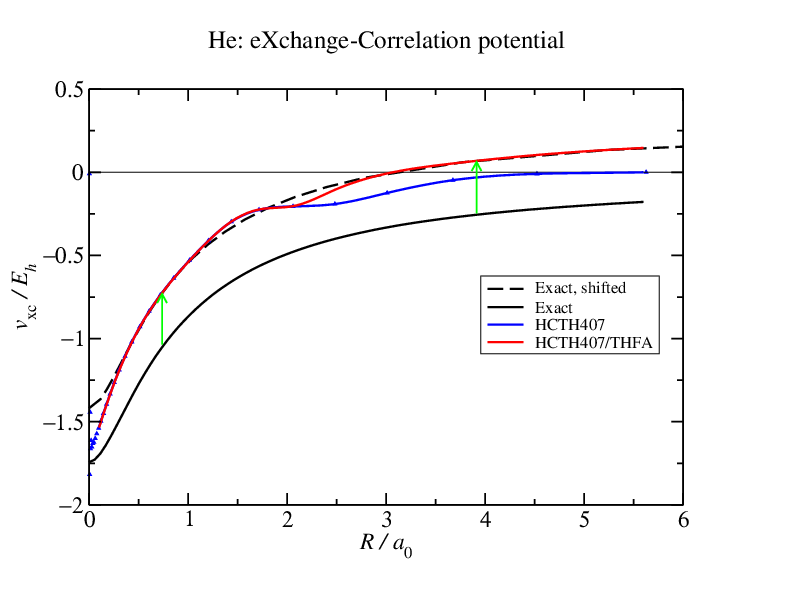So what we do is we apply an asymptotic correction: we know that the exact decay of the potential should be $-1/r$ so we enforce it by splicing a functional that decays as $-1/r$ to the exchange-correlation potential. This could be the Fermi-Amaldi exchange integral: $ {\rm FA}(r) = - \frac{1}{N} \int \frac{\rho(r')}{|r-r'|} dr' $

or using the LB94 exchange-correlation functional which has been constructed to result in a potential that decays as $-1/r$.

So why not just use LB94 for everything? This has to do with the shift. All local and semi-local functionals must be shifted w.r.t. the exact potential. I'll explain why when I get a chance. Well, if they are not shifted, then things go wrong. And LB94 goes wrong. But it can be used, with a suitable shift (based on the vertical ionization energy and HOMO eigenvalue), to fix approximate exchange-correlation potentials like HCTH407 as shown in the last figure. And this works very well indeed.

The asymptotic correction is needed to correct the tails of the exchange-correlation potential, and consequently, the density tails that are crucial for intermolecular interactions. In order to implement the asymptotic correction, accurate vertical ionization potentials (IPs) are needed for the monomers. When they are not available experimentally, good estimates may be obtained from the difference between the energies of the $N$ and $N-1$ electron systems. The PBE0 functional is best suited for this calculation too as tests on atoms, diatoms, and small organic molecules have shown that it gives IPs with mean errors centred about 0.0 a.u. with a standard deviation of only 0.007 a.u. ((Ernzerhof:99)). This correction is definitely needed if the individual interaction energy components are required to be accurate. However, it is cumbersome to apply for large systems, when a single IP may be questionable and local IPs are hard to define. In such cases, the asymptotic correction is best neglected, particularly if total interactions are all that is desired.