Contents
Index:
Interaction energy components and their Interpretation
At second-order in perturbation theory we have four interaction energy components that have well-defined physical interpretations.
Electrostatic energy
This is the first-order, classical interaction of the two unperturbed charge densities:
$\begin{align} E_{\rm elst}^{(1)} = \iint \rho_{A}(r_1) \frac{1}{\left|r_1 - r_2\right|} \rho_{B}(r_2) dr_1 dr_2. \label{eq:E1elst} \end{align}$
If we knew these densities this term would be trivial to compute. The electrostatic energy is perhaps the most important term - one which we should try to get right before developing elaborate models for the other interaction energy components.
First-order exchange-repulsion
The other first-order term is $E_{\rm exch}^{(1)}$. I will not provide an expression for this term just yet. It arises from the antisymmetry of the dimer wavefunction and is a repulsive term. This term depends on the unperturbed molecular wavefunctions (not the densities), but can be approximated using a density-based overlap model. More on this when I get a chance to elaborate.
Second-order induction energy
This is the sum of two terms: what is usually known as $E_{\rm ind,pol}^{(2)}$ and its exchange counterpart $E_{\rm ind,exch}^{(2)}$. However, as neither is physical on its own, I will add them together to give
$\begin{align} E_{\rm ind}^{(2)} &= E_{\rm ind,pol}^{(2)} + E_{\rm ind,exch}^{(2)}.\end{align}$
and will refer to this combined energy as the //induction energy//.
The induction energy can be interpreted as the second-order response of a molecule to the full (electonic and nuclear) potential of its interacting partners. Imagine it as follows: a polarizable (quantum) molecule is placed in a field. It's energy lowers by distorting in response to the field. Only this is not all that happens as this is a quantum system and the field includes singularities where the surrounding nuclei sit. Electrons can tunnel into these singularities - a purely quantum phenomenon - leading to what we call charge-transfer. I don't like this term and prefer //charge delocalization//, but more on this elsewhere.
In summary, the induction energy includes two kinds of effects:
- Polarization : this is a classical effect.
- Charge-Transfer : this is a purely quantum effect.
Second-order dispersion
As with the induction, the dispersion energy is the sum of two components:
$\begin{align} E_{\rm disp}^{(2)} &= E_{\rm disp,pol}^{(2)} + E_{\rm disp,exch}^{(2)}. \end{align}$
The two together give us the physical dispersion (sometimes called //van der Waals//) energy.
The dispersion energy is a purely quantum effect. It can be interpreted as the quantum energy stabilization through the correlation of spontaneous quantum fluctuations of the charge densities of the molecules. This is represented as follows:
What are these quantum fluctuations? Think of it like this: if matter was classical, then the dipole moment of a single helium atom would zero. After all, the dipole moment of a perfectly spherical charge distribution is zero. But atoms are not classical. Our measurements will be something like this:
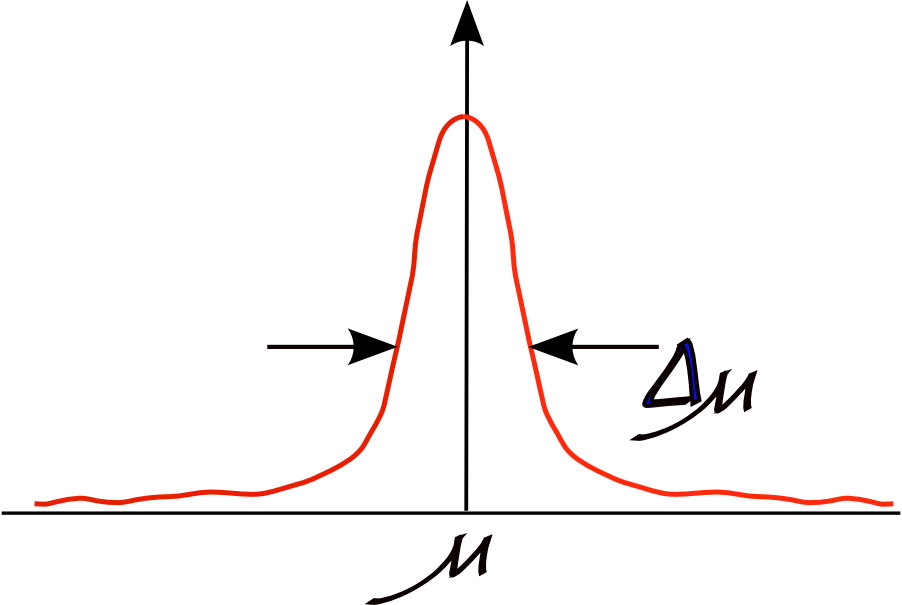
I.e., we get a distribution about zero. And nothing we do will reduce the width of this distribution. We can interpret this result by thinking of a quantum helium atom not as a static sphere, but as a charge density fluctuating about a sphere. Spontaneous charge distortions can result in an instantaneous dipole moment. Of course, it doesn't stop here: we can have higher ranking moments too but we will often talk of the dipole term only on the understanding that, as the leading order term it is the most important, but other terms are often quite important too.
Now, if we have two helium atoms in proximity, then an instantaneous dipole on one can //induce// a dipole on the other. This induced dipole then interacts with the original instantaneous dipole, leading to a nett reduction in energy. This is illustrated here (sorry, the dipoles should point in the other direction):
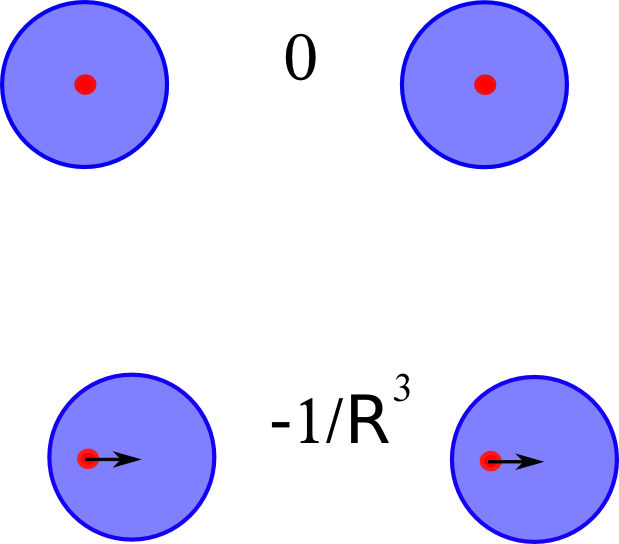
The field from an instantaneous dipole goes as $R^{-3}$ so the induced dipole has a strength proportional to this, and it, in turn, interacts with the original instantaneous dipole via another giving another $R^{-3}$ term, so we get the leading order dispersion //between a pair of atoms// goes as $-R^{-6}$. The minus sign indicates that this is an energetically favourable interaction.
I have emphasised that this is the leading order dispersion between a pair of atoms. The dispersion interaction between extended systems can be very different!
