Contents
Index:
Intermolecular systems: Examples
Here's a plot of the interaction energy between a pair of helium atoms: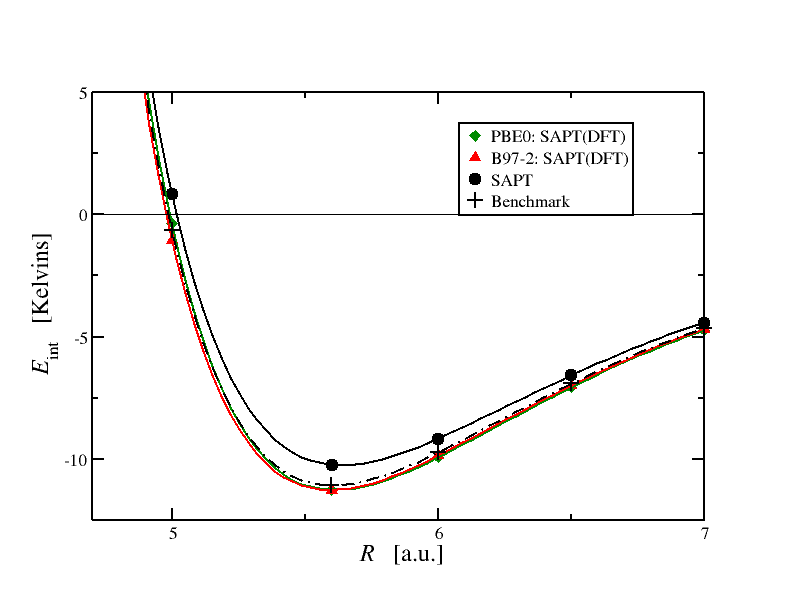 
There were three different kinds of calculations used to obtain these energies and they give slightly different energies. But more on that later. For now, observe the shape of the curve: there is a repulsive part at short range that arises from the exchange energies. Then we have an attractive minimum and then the energy tends to zero at long range. In this particular case the dispersion energy is responsible for the minimum. However in other systems the electrostatic and induction terms can also contribute a lot.
Here are interaction energy components for the water dimer, benzene dimer and the Cl$_2\cdots$OH$_2$ complex. The water dimer is in its equilibrium geometry, the benzene dimer is in the parallel stacked geometry with centre-of-mass separation 3.7 Angstrom, and the Cl$_2\cdots$OH$_2$ complex is in a symmetrical complex with all atoms in a plane and Cl-Cl$\cdots$O collinear with $r$(Cl$\cdots$O)$=2.755$ Angstrom. All energies are reported in kJ/mol.
Energy |
(H$_2$O)$_2$ |
Cl$_2\cdots$OH$_2$ |
(C$_6$H$_6$)$_2$ |
Perturbation Theory [SAPT(DFT)]: |
|||
$E_{\rm elst}||{(1)}$ |
$-28.90$ |
$-19.24$ |
$-19.24$ |
$E_{\rm exch}||{(1)}$ |
$+23.97$ |
$+24.96$ |
$+20.99$ |
$E_{\rm ind}||{(2)}$ |
$-5.16$ |
$-3.88$ |
$-0.95$ |
$E_{\rm disp}||{(2)}$ |
$-8.34$ |
$-10.73$ |
$-26.14$ |
$\Delta||{3-\infty}$ |
$-2.82$ |
$-3.24$ |
$+0.34$ |
$E_{\rm int}$ |
$-21.26$ |
$-12.13$ |
$-7.39$ |
Supermolecular MP2: |
|||
|
$-20.34$ |
$-12.43$ |
$-15.23$ |
Supermolecular CCSD(T): |
|||
|
$-20.45$ |
$-11.21$ |
$-7.57$ |
Notice that these complexes are bound in very different ways. All systems have significant dispersion components, but in the benzene dimer the dispersion is by far the largest. This complex is what is called a //dispersion bound// complex.
The water dimer is usually considered to be bound by electrostatic interactions, but perhaps this is an oversimplification. The structure of the dimer 
is surely determined by the electrostatic interactions, but the binding in this dimer arises predominantly from the dispersion, with a significant contribution from the induction at second and higher orders. What about the large electrostatic energy? It is mostly cancelled by the also very large first-order exchange-repulsion energy.
The halogen-bonded Cl$_2\cdots$OH$_2$ complex is intermediate between these two. This complex is bound by the dispersion and induction (at second and higher orders), though the geometry of this system may well be determined by the exchange-repulsion ((Stone, JACS 2013)).
The table contains three ways of calculating the interaction energies:
SAPT(DFT) is a symmetry-adapted perturbation theory (SAPT) based on density functional theory (DFT) and time-dependent density functional theory (TDDFT). SAPT(DFT) was developed by Misquitta (that's me), Szalewicz & Jeziorski ((Misquitta SAPT(DFT) papers to come here)) and, curiously, simultaneously by a colleague of mine, Andreas Hesselmann and Georg Jansen from Essen ((Hesselmann & Jansen papers here)). I guess the time was right for the development of this theory so the two groups, working on either side of the Atlantic, developed it independently.
- The other two methods are MP2 (Moller-Plesset perturbation theory at second order) and CCSD(T) (coupled-cluster with singles and doubles and non-iterated triples). These two give us only a single number: the interaction energy. They fall under the category of //supermolecular// methods.
Which one you'd choose depends on what you are after. MP2 is clearly no good for the benzene dimer. In fact, MP2 should probably be used for hydrogen-bonded systems only. If the dispersion interaction is known to be strong MP2 should be used carefully - if at all. In general, SAPT(DFT) and CCSD(T) are very similar in accuracy, but SAPT(DFT) is considerably faster as it involves a computational cost that scales as $\mathcal{O}(N^5)$ while CCSD(T) has a cost that scales as $\mathcal{O}(N^7)$.